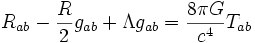Уравнение Эйнштейна

Общая теория относительности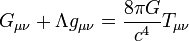

$G_{\mu \nu} + \Lambda g_{\mu\nu} = {8\pi G\over c^4} T_{\mu \nu}\,$

Математическая формулировка ОТО Космология Фундаментальные идеи Специальная теория относительности Пространство-время Принцип эквивалентности Мировая линия · Псевдориманова геометрия Явления Задача двух тел в ОТО · Гравитационное линзирование · Гравитационные волны Увлечение инерциальных систем отсчёта · Расхождение геодезических Горизонт событий · Гравитационная сингулярность Чёрная дыра Уравнения Линеаризованная ОТО Параметризованный постньютоновский формализм Уравнения Эйнштейна Развитие теории Теории типа Калуцы — Клейна Квантовая гравитация Теории гравитации Точные решения ОТО Шварцшильда Райсснера — Нордстрёма · Керра Керра — Ньюмена · Решение Гёделя Казнера · Модель Милна · Фридмана — Леметра — Робертсона — Уолкера Известные учёные Эйнштейн · Минковский · Шварцшильд · Леметр · Эддингтон · Фридман · Робертсон · Керр · Чандрасекар · Хокинг и другие…

Уравне́ния Эйнште́йна (иногда встречается название «уравнения Эйнштейна-Гильберта»^[1]) — уравнения гравитационного поля в общей теории относительности, связывающие между собой метрику искривлённого пространства-времени со свойствами заполняющей его материи. Термин используется и в единственном числе: «уравне́ние Эйнште́йна», так как в тензорной записи это одно уравнение, хотя в компонентах представляет собой систему уравнений.

Выглядят уравнения следующим образом:

$R_{ab} - {R \over 2} g_{ab} + \Lambda g_{ab} = {8 \pi G \over c^4} T_{ab}$

где R_ab — тензор Риччи, получающийся из тензора кривизны пространства-времени R_abcd посредством свёртки его по паре индексов, R — скалярная кривизна, то есть свёрнутый тензор Риччи, g_ab — метрический тензор, Λ — космологическая постоянная, а T_ab представляет собой тензор энергии-импульса материи, (π — число пи, c — скорость света в вакууме, G — гравитационная постоянная Ньютона). Так как все входящие в уравнения тензоры симметричны, то в четырёхмерном пространстве-времени эти уравнения равносильны 4·(4+1)/2=10 скалярным уравнениям.

Одним из существенных свойств уравнений Эйнштейна является их нелинейность, приводящая к невозможности использования при их решении принципа суперпозиции.

Исторический очерк

Работа Эйнштейна над теорией гравитации (общей теорией относительности), в одиночку и в соавторстве с рядом людей, длилась с 1907 года. В середине этих усилий Эйнштейн понимает, что роль гравитационного потенциала должен играть псевдо-риманов метрический тензор на четырехмерном пространстве-времени, а уравнение гравитационного поля должно быть тензорным, включающим тензор римановой кривизны и тензор энергии-импульса в качестве источника поля, сводясь в пределе малых энергий и стационарных полей к уравнению Пуассона ньютоновской теории гравитации. Затем, в 1913 году вместе с Гроссманом получает первый вариант таких уравнений (уравнения Эйнштейна-Гроссмана), к сожалению, совпадающий с правильным только для отсутствия вещества (или для вещества с бесследовым тензором энергии-импульса).

Летом 1915 года он приехал в Гёттингенский университет, где прочитал ведущим математикам того времени, в числе которых был Гильберт, один из главных их лидеров того времени, лекции о важности построения физической теории гравитации и имевшихся к тому времени у него наиболее перспективных подходах к решению проблемы и ее трудностях. Между ними завязалась переписка с обсуждением данной темы, которая значительно ускорила завершение работы по выводу окончательных уравнений поля. До недавнего времени считалось, что Гильберт получил эти уравнения на 5 дней раньше, но опубликовал позже: Эйнштейн представил в Берлинскую академию свою работу, содержащую правильный вариант уравнений, 25 ноября, а заметка Гильберта «Основания физики» была озвучена 20 ноября 1915 года на докладе в Гёттингенском математическом обществе и передана Королевскому научному обществу в Гёттингене, за 5 дней до Эйнштейна (опубликована в 1916 году). Однако в 1997 году была обнаружена корректура статьи Гильберта от 6 декабря, из которой видно, что Гильберт выписал уравнения поля в классическом виде не на 5 дней раньше, а на 4 месяца позже Эйнштейна.^[2]. В ходе завершающей правки Гильберт также вставил в свою статью ссылки на параллельную декабрьскую работу Эйнштейна.^[1]

Сначала уравнения Эйнштейна решались приближённо, в частности, из них были выведены как классическая теория Ньютона, так и поправки к ней. Первые точные решения были получены Шварцшильдом для центрально-симметричного случая. Ряд решений были вскоре выведены в рамках релятивистской космологии.

См. также

• Математическая формулировка общей теории относительности
• Точные решения уравнений Эйнштейна

Литература

• Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7

Примечания

1. ↑ ^{1 2} Сам Гильберт никогда не претендовал на авторство этих уравнений и безоговорочно признавал приоритет Эйнштейна. См. подробности в статье: Эйнштейн, Альберт#Гильберт и уравнения гравитационного поля.
2. ↑ Визгин В. П. Об открытии уравнений гравитационного поля Эйнштейном и Гильбертом (новые материалы). УФН, № 171 (2001), стр. 1347.